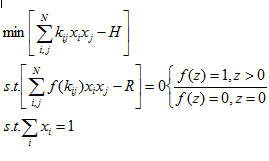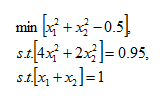A blog exploring topics of software development with specific focus on effective communication between the disciplines involved in the software lifecycle; and ways to solve some select mathematical problems using the .NET framework as a base, specifically coding in C#. This will document a learning journey shared by the author (me) and the readers (you and all your lovely friends) alike
Tuesday, 31 March 2015
Quantum Fork
What? you may ask. Well, as I mentioned in the post yesterday the need to clearly and effectively communicate ideas, requirements and specifications is vital to a successful software project delivery, and vital to the sanity of the developers by removing the pressure from managers to quantify what is clear to a dev but not others. So this blog is taking a change, a fork you may say. The investigation of techniques for solving complex maths problems will continue, but alongside that will be a discussion of methods to communicate between members of an interdisciplinary team (and with those outside the team) in a clear way, preferably without the need to 'translate' the information for each audience member. Quantum Fork as you can follow both paths simultaneously, think of yourself as a superposition of readers.
The decision to rename the blog and include posts on both subjects was made so that you will all reap the benefit of getting all the content I put out, and I will get the benefit of not losing you as readers due to a change or URL.
I look forward to posting my first communication themed musings over the next week.
Monday, 30 March 2015
Need for Visualisation
Due to time constraints I have not managed to get a working system to display these results in a way that I would like, so I am not including the details in this post, but they will come soon.
The problem of describing a problem like the one we are attempting to solve is always going to be a difficult one, and is just one example of the difficulty in communicating within a multidisciplinary environment. Not only do we have managers that need results, and want detailed explanations of timescales to get results with tangible progress indicators; we need to ensure that the needs of the system as outlined by business analysts are understood by devs and testers alike, and that end users can be provided with useful documentation, and, and, and. The channels are endless, and that brings its own problems. I will be looking at this set of problems in either this blog or a sister blog soon, and I will provide a link if necessary when it comes about.
Thursday, 12 March 2015
Implementing a Breeding Algorithm
Averaging Operator
The first and simplest breeding operator I could think of is one where the value of each gene is an average of the corresponding values in the parents:
| Chromosome | Gene 1 | Gene 2 |
|---|---|---|
| Parent 1 | 3 | 6.2 |
| Parent 2 | 5 | 4.1 |
| Child | 4 | 5.15 |
One problem with this is that it will instantly violate the simple sum of gene values constraint we imposed. As such the actual code goes a step further and 'normalises' the genes of the child chromosome to have a sum that matches that of the parents.
This operator is not a true breeding operator in its purest form as it does modify the values of the genes rather than simply create a new chromosome by resequencing genes selected from the parents. As such it is more of a breeding and mutation operator in one. The reason behind the decision to do this was that in a continuous variable problem, the best solution may possibly exist in a space 'between' the solutions that have already been explored, so a mutation and a resequencing combined may help to explore the problem space more rapidly. Remember that in the first post a single point crossover breeding operator was used, this takes part of each parent and concatenates to form a child, the table below showing how the same parents can produce 2 different children by changing the point of crossover
| Chromosome | Gene 1 | Gene 2 | Gene 3 | Gene 4 |
|---|---|---|---|---|
| Parent 1 | 1 | 2 | 3 | 4 |
| Parent 2 | 9 | 8 | 7 | 6 |
| Child | 1 | 2 | 7 | 6 |
| Child | 1 | 8 | 7 | 6 |
and we have the results of this non-mutating breeding operator to compare with those of a hybrid breeder-mutator operation.
Results do show that this operator gives no noticeable advantage over the out of the box pure crossover operation, with R=0.941 and F=0.235 with the SwapMutate operator unmodified from the first post.
the code for this operator is:
public void Invoke(Population currentPopulation, ref Population newPopulation, FitnessFunction fitnesFunctionDelegate)
{
Debug.WriteLine("Breeding from pop size of {0} into pop size of {1}", currentPopulation.PopulationSize, newPopulation.PopulationSize);
//first check sixe of new population, if its big enough already just return
if (newPopulation.PopulationSize >= currentPopulation.PopulationSize)
return;
//also cannot perform with less than 2 chromosomes
if (currentPopulation.PopulationSize < 2)
return;
while (newPopulation.PopulationSize < currentPopulation.PopulationSize)
{
//otherwise take 2 chromosomes at random from the current population (include elite ones)
var parents = currentPopulation.Solutions.SelectRandomMembers(2);
//craete the new chromosome
//assumes both parents have the same the sum of gene values
var sum = parents.First().Genes.Sum(g => g.RealValue);
var newGenes = new List<double>();
for (int i = 0; i < parents.First().Genes.Count; i++)
{
newGenes.Add((parents.First().Genes.ElementAt(i).RealValue + parents.Last().Genes.ElementAt(i).RealValue) / 2);
}
//now normalise to the same sum
var newsum = newGenes.Sum();
var m = sum / newsum;
var ch = new Chromosome(newGenes.Select(g => g * m));
newPopulation.Solutions.Add(ch);
}
}
Normalised Sum Operator
A slight variation on the averaging breeder is to instead simply sum the gene values of the parents, then 'normalise' the sum of gene values to meet the constraint. Again this does not offer any great advantage with R=0.978 and F=0.244
from code
public void Invoke(Population currentPopulation, ref Population newPopulation, FitnessFunction fitnesFunctionDelegate)
{
Debug.WriteLine("Breeding from pop size of {0} into pop size of {1}", currentPopulation.PopulationSize, newPopulation.PopulationSize);
//first check sixe of new population, if its big enough already just return
if (newPopulation.PopulationSize >= currentPopulation.PopulationSize)
return;
//also cannot perform with less than 2 chromosomes
if (currentPopulation.PopulationSize < 2)
return;
while (newPopulation.PopulationSize < currentPopulation.PopulationSize)
{
//otherwise take 2 chromosomes at random from the current population (include elite ones)
var parents = currentPopulation.Solutions.SelectRandomMembers(2);
//craete the new chromosome
//assumes both parents have the same the sum of gene values
var sum = parents.First().Genes.Sum(g => g.RealValue);
var newGenes = new List<double>();
for (int i = 0; i < parents.First().Genes.Count; i++)
{
newGenes.Add(parents.First().Genes.ElementAt(i).RealValue + parents.Last().Genes.ElementAt(i).RealValue);
}
//now normalise to the same sum
var newsum = newGenes.Sum();
var m = sum / newsum;
var ch = new Chromosome(newGenes.Select(g => g * m));
newPopulation.Solutions.Add(ch);
}
Conclusion
Although the operators selected for use in the algorithm obviously do have a factor in the obtaining of a good solution, it appears that they do not have a significant impact on just how good a solution can be found. It may be a leap of faith at this stage but it is my belief that the fitness calculation will have a far more significant impact, and that is something that I will explore in the next post.
And on that theme, the next post may possibly be delayed as I am currently in hospital and have no access to my PC to do any coding, but hopefully I will get my hands dirty again fairly soon and be able to produce another post.
Tuesday, 10 March 2015
Implementing a mutation algorithm
- How do we vary the genes?
- How many genes in a chromosome should change in a given mutation?
- What if a mutated chromosome is unviable?
New Mutations
I will look at 2 mutation operators in this post, and detail the results of using each. The first of these mutation operators simply takes a single gene of a chromosome, modifies its value and adjusts the other genes so that the constraint of the sum of gene values remains a constant. In practise this operator will select a proportion of the population of solutions not tagged as being elite solutions (elite solutions are earmarked to remain unchanged between generations) and mutate these. The code I implemented to test this mutation is:
1: public void Invoke(Population currentPopulation, ref Population newPopulation, FitnessFunction fitnesFunctionDelegate)
2: {
3: var eliteCount = newPopulation.Solutions.Count(ch => ch.IsElite);
4: var numberToMutate = (int)System.Math.Round((newPopulation.PopulationSize - eliteCount) * MutationProbability);
5: newPopulation.Solutions
6: .Where(ch => !ch.IsElite) //get the non elite
7: .Take(numberToMutate) // selct the right percentage of these
8: .ToList()
9: .ForEach(ch => DoMutate(ch));
10: }
11: private void DoMutate(Chromosome ch)
12: {
13: //need to select a value from the chromosome mutate then ensure the sum is maintained
14: var geneIndexToMutate = rand.Next(ch.Genes.Count);
15: var gene = ch.Genes.ElementAt(geneIndexToMutate);
16: //now change this value, it must have a new value of less than SumOfGenes, so
17: var newGene = new Gene(rand.NextDouble() * SumOfGenes);
18: //and now modify the others, so find new sum, what do we need to multiply this by to get 1??
19: var m = 1d / ch.Genes.Except(new []{gene}).Sum(g => g.RealValue) + newGene.RealValue;
20: newGene = new Gene(newGene.RealValue * m);
21: //now multiply every gene By this to get mutated chromosome with correct sum
22: var AllNewGenes = ch.Genes.Take(geneIndexToMutate)
23: .Select(g => new Gene(g.RealValue * m))
24: .Concat(new[] { newGene })
25: .Concat(ch.Genes.Skip(geneIndexToMutate + 1)
26: .Select(g => new Gene(g.RealValue * m)))
27: .ToList();
28: ch.Genes.Clear();
29: ch.Genes.AddRange(AllNewGenes);
30: //Debug.WriteLine("New Sum {0}", ch.Genes.Sum(g => g.RealValue));
31: }
The mutation requires knowledge of the sum of gene values constraint, and this is set on the construction of the operator, this can be seen as a shortcoming of the operator for general use, but for the purposes of investigating the effects of value mutation on chromosomes made up of a set of continuous variables, I have chosen to overlook this.
The results of using this operator are not as impressive as one would possibly expect. Using the out of the box SwapMutator values of R=0.988 and F=0.247 are found. Using the new mutation operator, R=0.993 and F=0.248 are found. A slight improvement in the objective mimisation, with a loss in the constraint. Now this is a very simplistic mutation of the gene values, with no memory of the previous value retained or used in the mutation. As such I thought I should try another variation on the operator
17: var mult = (minMultiplier + this.range * rand.NextDouble());
18: var newGene = new Gene( mult * geneValue);
where minMultiplier +this.range will give a value between 0.5 and 1.5 based on a range value between 0 and 1. This produces results of R=0.995 and F=0.248 for a range of 0.9; and R=0.990, F=0.247 for a range of 0.2.
So the retention of some of the parent's identity does not seem to help.
Mutate by Pairs
The second mutation I chose to try was the mutation of a chromosome by changing a pair of genes and leaving all others untouched. By this method the sum of the genes values could be maintained by careful selection of the new values. The code to perform this mutation is very similar:
1: public void Invoke(Population currentPopulation, ref Population newPopulation, FitnessFunction fitnesFunctionDelegate)
2: {
3: var eliteCount = newPopulation.Solutions.Count(ch => ch.IsElite);
4: var numberToMutate = (int)System.Math.Round((newPopulation.PopulationSize - eliteCount) * MutationProbability);
5: newPopulation.Solutions
6: .Where(ch => !ch.IsElite) //get the non elite
7: .Take(numberToMutate) // selct the right percentage of these
8: .ToList()
9: .ForEach(ch => DoMutate(ch));
10: }
11: private void DoMutate(Chromosome ch)
12: {
13: if (ch.Genes.Count <=1) return;
14: //need to select a value from the chromosome mutate then ensure the sum is maintained
15: var geneIndexToMutate = rand.Next(ch.Genes.Count / 2);
16: var geneIndexToMutate2 = geneIndexToMutate;
17: while(geneIndexToMutate>=geneIndexToMutate2)
18: geneIndexToMutate2 = rand.Next(ch.Genes.Count / 2, ch.Genes.Count);
19: //now change this value, it must have a new value of less than SumOfGenes, so
20: var newVal1 = -1d;
21: var newVal2 = -1d;
22: while(newVal1 <=0 || newVal2 <=0)
23: {
24: newVal1 = rand.NextDouble();
25: newVal2 = (ch.Genes.ElementAt(geneIndexToMutate).RealValue+ ch.Genes.ElementAt(geneIndexToMutate2).RealValue) - newVal1;
26: }
27: //and now modify the others, so find new sum
28: var AllNewGenes = ch.Genes.Take(geneIndexToMutate)
29: .Concat(new[] { new Gene(newVal1) })
30: .Concat(ch.Genes.Skip(geneIndexToMutate + 1)
31: .Take(geneIndexToMutate2 - geneIndexToMutate - 1))
32: .Concat(new[]{ new Gene(newVal2) })
33: .Concat(ch.Genes.Skip(geneIndexToMutate2 + 1))
34: .ToList();
35: ch.Genes.Clear();
36: ch.Genes.AddRange(AllNewGenes);
37: //Debug.WriteLine("New Sum {0}", ch.Genes.Sum(g => g.RealValue));
38: }
which gives results of R=0.989 F = 0.247.
Conclusions
So it appears that the form of the mutation is not the limiting factor in finding a good solution to the problem. There may well be a better mutation possible, but the quality of the mutation id more likely to impact on the speed of convergence (not strictly a convergence as its a pseudo random exploration of the problem space) rather than the final result.
In coming posts I will explore the use of different breeding operators and finally the effect of the fitness calculation on the final result.
Wednesday, 4 March 2015
Interlude - Why a blog?
You may think 'interlude, but we just started, I don't need a break yet, give me more!' and you would be right. This post comes now because I should have written it first, or put some of the contents in to the first post, but I was excited about getting some ideas down on paper to make a starting point for our learning journey in the potential use of GA that I couldn't hold back. So I am writing it now as an aside to my ongoing work on GA.
So why write a blog?
I started writing this blog for a number of reasons, I know from past experience that the best way to get a good understanding of something new is to try to explain it to others. Teaching is the best way to learn. So that was a nice selfish reason. My day job is a bit mundane at present, a lot of repetitive coding, so a more interesting distraction mentally is welcome. And the reason why now, is that I joined John Somnez's blogging course to give myself the boot up the backside to do more. He gives a load of reasons why writing a blog is a good idea, mostly based around self promotion, career progression and money. All very important factors in the life of a software dev, and all have their place in my list of priorities, but above all else I love to learn and challenge myself. I also recently started a non-software blog on my personal life (diagnosed with MS recently) and I am enjoying writing that immensely, so a software based blog I thought would be a great idea to keep my mind fresh on interesting dev topics, and importantly dev topic I care about.
John's blogging course is a very useful education tool, very informative, easy to follow and eloquent in its encouragement for everyone to get blogging, go and give it a read, and if you start blogging let me know I love to read what others are doing (after all that how I got here by reading John's blog)
Next post will be back on topic
Monday, 2 March 2015
Can a Genetic Algorithm Approach Solve a Continuous Variable Minimisation Problem?
Please don't be put off by the maths at this stage, I am simply looking to set the scene, I will not be delving into equations, rather the concepts of solving a class of problems. Essentially I had an equation something like:
with this example being a simplified version in 2 dimensions, the real problem I was tackling had 19 dimension, but the concept is the same.
To give some real values to the problem for those of us who don't think in terms of pure mathematics, my simplest test scenario involved having a limit of N = 2 a matrix for k of
setting the values of H and R to be 0.5 and 0.95 respectively, we have
which on the face of it seems fairly straightforward. Brute force should make it fairly easy to solve, it can be reduced to a one dimensional problem, and very basic techniques could be used to solve. But without going to town on expanding the problem, imagine adding a third dimension, or simply increasing N to 3.
There are many techniques out there for solving such constrained non-linear minimisation problems, such as the use of Lagrange multipliers or numerical approaches like interior point interpolation. However I was, and still am interested in whether using genetic algorithms could be a fruitful avenue of investigation for this category of problem.
Genetic algorithms have a number of advantages over purely mathematical approaches. The problem of local minima being found being a key one, and from a computational point of view, the scalability of a GA approach drew me in.
What is a Genetic Algorithm
The idea behind a GS Approach is that given a problem that we have no idea of how to get to a good solution of, but where we know a good solution when we see it, we can explore the problem space finding progressively 'better' solutions until such a time as we are satisfied with the best solution tested.
In practice this means that we need to have a way to evaluate how 'good' a solution to the problem is. For the problem described earlier, we need a way to determine if for a given set of x the solution is acceptable, and how good a solution it is. As we have a constrained problem, only solutions for which the 2 constraint equations are satisfied are permissible. A simple measure of how good each permissible solution is would be how far from 0 the minimisation part resolves to.
Given this ability to evaluate how good a solution is (known as the fitness of the solution) the algorithm needs a way to generate new potential solutions in an educated manner to find ever better solutions, and then to iterate this loop.
The term genetic algorithm takes its origins from Darwinian evolutionary theory. A population of potential solutions exists, from which the fittest are selected, a further generation of solutions is born (variation in the population created via cross breeding and mutation), the weakest being culled, the fittest surviving, reproducing and evolving through the generations.
Given a broad enough initial population and sufficient generations, all corners of the problem space should be explored, with good, but not necessarily the best solutions not swamping out rarer but stronger strains.
Seems ideal?
Yes it does, calculating the fitness of a solution in this way is very fast and cheap. The calculation of the fitness of any solution is an atomic process, so a huge population is not a problem as we can easily scale out. So what is the problem and why aren't all mathematical problems approached this way?
One problem comes that a solution may be investigated that is a poor fit and discarded, another that is a fair but not excellent fit is returned in preference. over time we get a healthy population of fair solutions, but nothing good enough. Through mutation an cross breeding we will always continue to explore new solutions until the algorithm exits, however the details of the breeding and mutation limit the ability to find an 'ideal' solution.
The mere fact that we have discarded any possibility of a solution that violates the constraint equations out of hand means that we may be ruling out entire sections of the problem space that could evolve to yield a better solution.
A post that explores the idea of constraints that tighten through the generations is here, and suggests that ruling out solutions early in the evolutionary process is a bad idea, with solutions that violate the constraints becoming less favourable in later generations, but in early generations having the opportunity to influence the overall population.
How to implement a GA in .NET
A very good question, you could spend years writing the evolution, mutation, breeding and selection code. However, good news, there is a great framework that does the hard work for you, allowing you to concentrate on the problem you are really interested in. Using GAF allows you to concentrate on evaluating the fitness of solutions, defining how the mutations occur and how breeding is performed. With only the need to define 2 functions (evaluate the fitness of a solution and determine if we should stop evolving) you can solve a problem. A good introduction to the framework is given here with examples of problems you can solve.
The specific functions I used for this problem are:
private static double CalculateFitness(Chromosome solution)
{
var tol =1e-3;
var unfit = 0;
//need to calculate the proximity of the three equations to 0
var sum = solution.Genes.Sum(x => x.RealValue);
if (System.Math.Sqrt(System.Math.Pow(sum - 1, 2)) > tol) return unfit;
if (GetDeltaR(solution.Genes.Select(x => x.RealValue)) > tol)
return unfit;
return 1d-(GetDeltaF(solution.Genes.Select(x => x.RealValue)));
}
Where GetDeltaR and GetDeltaF calculate the difference between the result of the calculation and 0, the returned fitness is best at 1 and a solution is totally unfit if this evaluates to 0.
private static double GetDeltaF(IEnumerable<double> enumerable)
{
return System.Math.Sqrt(System.Math.Pow(GetF(enumerable) - TargetF, 2));
}
private static double GetDeltaR(IEnumerable<double> enumerable)
{
return System.Math.Sqrt(System.Math.Pow(GetR(enumerable)-TargetR, 2));
}
and
private static bool Terminate(Population population, int currentGeneration, long currentEvaluation)
{
return currentGeneration > 400;
}
The decision to terminate is simply based on the number of generations here, only because experience has told me that this will not reach a solution where delta F is less than an acceptable level.
So it doesn't solve the problem?
Not as such. With the fitness calculation above and the choice of breeding and mutation algorithms (I used the out of the box single point crossover breeding and swap mutation provided by GAF) a very good solution is not found. However it does find a solution, and with some minor tweaks to only the fitness evaluation (taking into account the ideas of relaxed constraints in the linked article) a solution with R = 0.943 and F = 0.235 can be found in seconds. Clearly this is not an ideal solution, but it is pretty good as a first stab.
For a problem such as this, the key to getting a good solution is choosing the correct mutation algorithm and breeding process. The swap mutation used simply swaps round the elements of the solution, they do not 'vary', so a solution of (1,2) could mutate to (2,1) but could not become (1.1,1.9). As we are dealing with continuous variables, the inability to mutate in this way will limit the proximity to the solution that we can get.
The crossover breeding takes 2 solutions, and uses part of each to produce a child solution (e.g. 1,2 and 3,4 could become 1,4) which is acceptable given a suitable mutation and sufficient generations to explore all evolutionary branches.
I am interested in developing a new mutation algorithm that modifies the elements (termed genes in genetic algorithm circles) of the solution and will detail this process in a later blog.
Suffice to say with little effort using GA to solve a complex mathematical problem is a good way to go. The effort to get a truly 'good' solution, may be a little greater, but to get a solution there is little effort. I have previously attempted to solve the class of problems described here using interior point interpolation with some success, however the starting point of these interpolations is key to finding a good solution as they are very prone to finding local minima. As such, a hybrid approach may be the answer, with GA selecting a range of potential starting points from which to interpolate rather than using either approach in isolation.